This post will detail a closed form solution to split polygons into any number of equal areas, while ensuring minimum length of line based cuts. The solution works for both convex and concave polygons, as long as they don’t have non-manifold vertices, and can be traversed with a single loop. Credit for this concept goes to Dr. Rossignac, who also introduced me to the power of medial axis.
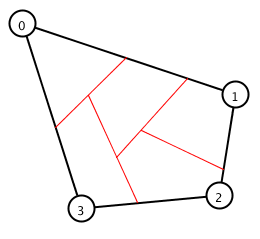
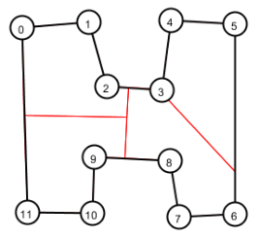
Figure 1: Examples of Convex (Left) and Concave (Right) Polygon division. Red lines show the cuts splitting polygons into equal areas
 |
 |
Base Case: 4-Sided Polygon
Let’s start with a 4-sided polygon, and say we need to split this into N sub-polygons. We use the divide and conquer methodology:
- Calculate the area of the polygon, say A_{poly}. Therefore the target area of each of the N sub-polygons would need to be A_{poly} \over N
- Split the polygon into two sub-polygons – smaller one with area of A_{poly} \over N, and bigger one with area of {(N-1)\over N} A_{poly}
- Continue using the same approach on the bigger polygon till the bigger polygon reduces into polygon with desired area.
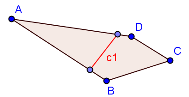
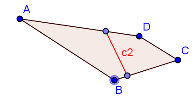
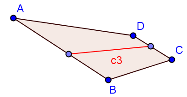
The problem of splitting polygon N-ways has now been reduced to splitting polygon into two sub-polygon with specific area. Since the cut is a line, it would start from one edge and end at another. There are six possible edge pairs in a 4-sided polygon, that could lead to a potential cut. Three of these cuts – C1, C2, C3 are shown in the images below as a reference. We can select the minimum cut from the all potential cuts obtained from each edge pair.
Figure 2: Three potential cuts for splitting polygon ABCD
 |
 |
 |
Now, the problem is reduced to making a cut on a given edge pair, such that the cut splits the polygon into two sub-polygons of specific area. Continue reading