This post will detail a closed form solution to split polygons into any number of equal areas, while ensuring minimum length of line based cuts. The solution works for both convex and concave polygons, as long as they don’t have non-manifold vertices, and can be traversed with a single loop. Credit for this concept goes to Dr. Rossignac, who also introduced me to the power of medial axis.
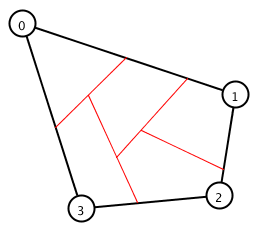
Figure 1: Examples of Convex (Left) and Concave (Right) Polygon division. Red lines show the cuts splitting polygons into equal areas
 |
 |
Base Case: 4-Sided Polygon
Let’s start with a 4-sided polygon, and say we need to split this into N sub-polygons. We use the divide and conquer methodology:
- Calculate the area of the polygon, say A_{poly}. Therefore the target area of each of the N sub-polygons would need to be A_{poly} \over N
- Split the polygon into two sub-polygons – smaller one with area of A_{poly} \over N, and bigger one with area of {(N-1)\over N} A_{poly}
- Continue using the same approach on the bigger polygon till the bigger polygon reduces into polygon with desired area.
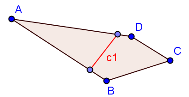
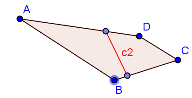
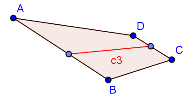
The problem of splitting polygon N-ways has now been reduced to splitting polygon into two sub-polygon with specific area. Since the cut is a line, it would start from one edge and end at another. There are six possible edge pairs in a 4-sided polygon, that could lead to a potential cut. Three of these cuts – C1, C2, C3 are shown in the images below as a reference. We can select the minimum cut from the all potential cuts obtained from each edge pair.
Figure 2: Three potential cuts for splitting polygon ABCD
 |
 |
 |
Now, the problem is reduced to making a cut on a given edge pair, such that the cut splits the polygon into two sub-polygons of specific area.
Splitting Polygon For a Given Edge Pair
Say, we select edges AD, and BC in the 4-sided polygon shown below.
- Determine the angle bisector of the edge pair. This is dotted line, labelled as m in the figure below.
- Determine the projected points of the four vertices on their corresponding opposing edge, at the angle perpendicular to the angle-bisector m
- Ignore the projected points that don’t lie on the opposing line segment. In the figure, the projected vertex of B is G, and D is H. The projection of point A along the line perpendicular to angle-bisector m doesn’t lie on edge BC, so it is ignored. Same argument applies to the projection of point C. The valid projection points of the four vertices are G, and H.
- Connect the vertices B, and D to their corresponding valid projection points G, and H. The polygon formed by the edge pair, is now a combination of triangles AGB, DCH, and trapezoid GDHB.
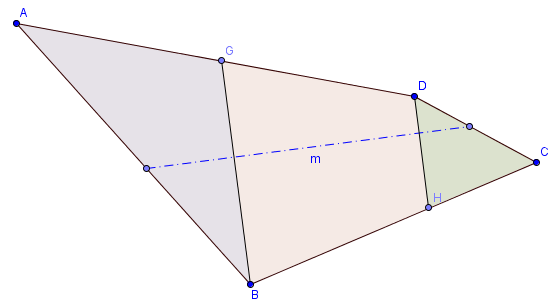
Figure 3: Splitting polygon for edge pair: AD and BC - The minimum cut, if it exists for this given edge pair, must lie in these two triangles or the trapezoid
- To find out where the minimum cut line lies, we can do a simple area check. Say, A_{AGB} is the area of the left triangle, A_{GDHB} is area of the trapezoid, and A_{DCH} is the area of the right triangle. The minimum cut line lies in the:
- Left Triangle, if A_{poly} \over N < A_{AGB}
- Trapezoid, if {A_{poly} \over N} > A_{AGB}, and {A_{poly} \over N} < {A_{AGB} + A_{GDHB}}
- Right Triangle, if {A_{poly} \over N} < {A_{AGB} + A_{GDHB}}
- Minimum Cut in a Triangle For a Given Edge Pair
Say, based on the area test, the minimum cut lies inside the left triangle, as shown in Figure 4. One end of the red cut line lies on the vertex B. The other end of the edge can be found by linear interpolation of points A, and G based on the target area. Since the target area is A_{poly} \over N, and the interpolated point will be A + {A_{poly} \over {N*A_{AGB}} }(G - A)
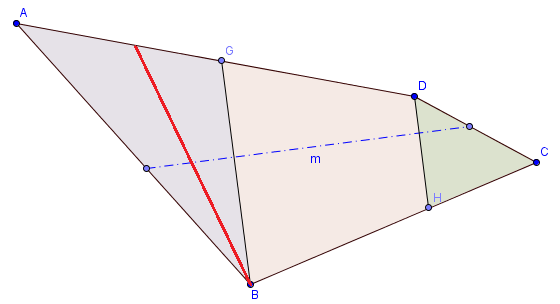
Figure 4: Minimum cut (Red Line), for a given edge pair lies in the triangle AGB - Minimum Cut in a Trapezoid For a Given Edge Pair
If the minimum cut lies in the trapezoid, then the two points of the split line (shown in red) can be found via linear interpolation based on the target area, similar to the approach we took for the triangle case above. In the case of triangle, one point of the split line was fixed as a vertex. In the case of trapezoid, both points of the red split line can move based on the area. However, the requirement that the split line needs to be minimum dictates that the angle of the split line must always be perpendicular to the angle-bisector of the edge pair. One end of the line will be the linear interpolation between points G, and D. The other end of the red line will be the linear interpolation between points B, and H.
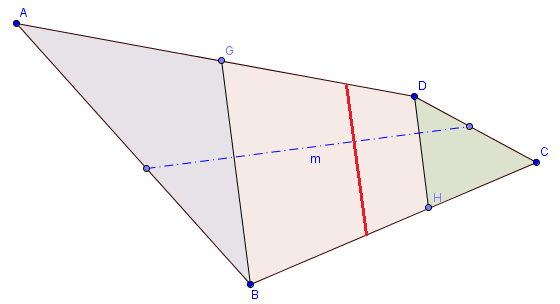
Figure 5: Minimum cut (Red Line), for a given edge pair lies in the trapezoid
Key Concept
For a given edge pair, the minimum cut line within a trapezoid, must lie perpendicular to the angle-bisector of the two edges in the edge-pair. While this makes sense intuitively, it can also be geometrically proved by creating a trapezoid where the parallel edges lie at an angle \alpha to the angle-bisector. The area of this trapezoid can be expressed as a function of \alpha. For the cut line to be minimum, we take the derivative of the area, and it can be shown, that for a given area, \alpha must be equal to 90^{\circ}
General Case: Splitting N-Sided Polygon
So far, we have shown, how to determine the minimum cut line for a given edge pair. We can easily extend this for any N-sided polygon
- For a given edge, we check all the other remaining edges, to see where a split line could exist
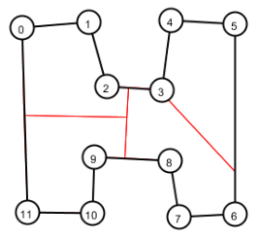
- The figure above shows a random polygon, and we have selected an edge pair AB, and CD
- There may be several edge pairs that provide a potential split cut. We can compare them, and select the minimum cut.
- Special Case: For concave polygons, some of the cut lines found with above approach will be outside the polygon and/or intersect with existing edges. So we simply add an additional verification step to ensure that the split lines don’t do so. If they do, then we ignore those split lines as a potential solution.
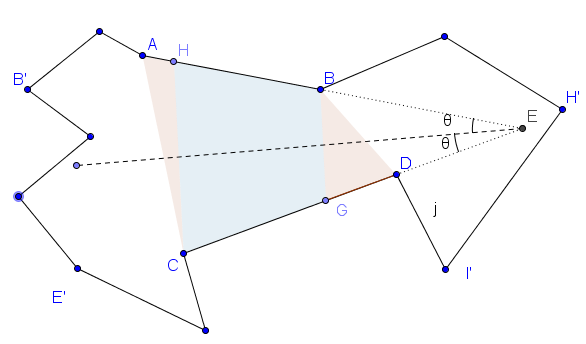
Figure 6: General case: splitting n-sided polygon
Time Complexity
Say, we want to split a 4-sided polygon into 4 sub-polygons. We start by splitting the polygon into two pieces one with {1/4}^{th} area, and another one with {3/4}^{th} area. The same process would then be repeated on the bigger sub-polygon till all sub-polygons are of target area. At each step of splitting into two sub-polygons, there are several possible edge pairs. For example, in the very first step, the 4-sided polygon has 6 possible edge pairs, and therefore 6 possible split lines. Each of these splits would lead to its own tree of final solution. Therefore we have two possible approaches:
- Greedy & Iterative Approach
We take the minimum cut at each step, and ignore the others. This approach may not always lead to the correct solution, but the results will be fast. The algorithm has cubic time complexity for convex polygons. Checking every edge pair requires quadratic complexity, and for a given edge pair, the algorithm involves calculating area, and doing linear interpolation for finding split lines. For concave polygons, another verification step, that involves ensuring split lines don’t intersect with other remaining edges, is needed. This additional step leads to quartic time complexity. - Comprehensive & Recursive Approach
In this approach, we consider every possible split generated by each edge pair at each step, and follow the trail from each split. Because of the recursive nature, the result is always correct, but the time complexity becomes exponential.
Implementation
The recursive approach as outlined above was implemented via processing. The video demo below shows how the split lines change in real time as polygon coordinates or number of required splits is modified.